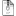Keno is usually a game where you choose 1 to 20 number between 1 and 80, then 20 number is chosen by the machine/casino. The payoff is determined by the amount of number you chose. The odds of keno can be a little confusing, due to its sheer amount of number you can choose and the fact that it is a draw without replacement. Keno has been dissected by some mathematicians and you can easily find some odds calculator for it on the net.
Grarrl Keno has however a little trick under its sleeve
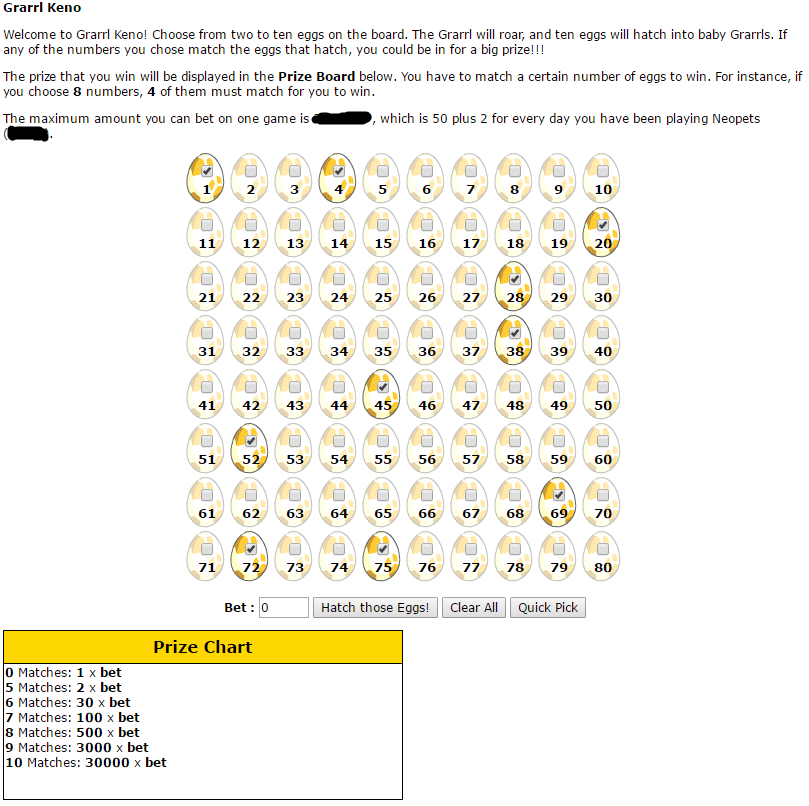
If you already played it, you know that there's only 10 draw. This makes all the difference since it horribly change the odds. So, how do we calculate the odds now, you may ask? Well, I found a calculator (I could have done it by hand, but you know, if there is already a program that makes it for you, might as well use it.) that makes calculation for any kind of draw without replacement. You can find the calculator here, if you don't mind French :x
A godsend tools for our purpose
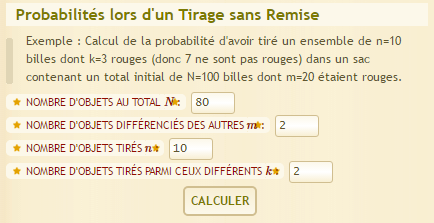
So now that we have the odds for each possible outcome, we can actually calculate the expected profit. I tripped over my choice of word in my other thread about Coconut Shy, but I'll explain what exactly is the expected profit and expected value for non-mathematics academic. The expected value, without going too deep in the subject, is a way to find the mean of a numeric outcome if the draw is infinite. The most notorious example is the expected value of a six sided dice, which is 3.5. That value means that if we roll the dice infinitely, the mean of the numeric outcome is 3.5.
Example of a six sided dice. As you can see, the formula is the sum of all
the outcome multiplied by their respective probability .
(Source of the picture: Wikipedia)
The expected profit is actually an application of the expected value. Some reference does not even makes a distinction between both of these terms. Instead of multiplying the different outcome of the random experiment with their respective probability, it is the profit that the outcome gives that you multiply by its probability. For example, if you bet 1$ on a game of head or tail, and if you win, you get 2.25$ back. You have 1/2 chance of losing 1$ and 1/2 chance of winning a profit of 1.25$. If you play infinitely, you can expect a profit of approximately 0.125$.

(Calculated with Maple 2015.1 Build 1059989)
Expected value and expected profit are heavily used in gambling and insurance industry. They are used in gambling to know how much the host win or lose per customer, if there is enough customer to be considered infinite (casino usually fit this description). We can use it to determine how much neopoints in average you lose or win per game while playing Grarrl Keno (spoiler alert: you don't win). Of course we need a really big number of play for this to be a good average, and no one will play that much, right? Unless... You're going for the avatar.

Oh, sweet sweet avie
Therefore, I made an Excel sheets that calculate the expected value for every amount of number chosen by the player, so I can laugh at those who chose 10 number and refreshed (or not, you probably make 1000 times the amount you loss, but oh well, I love statistics).
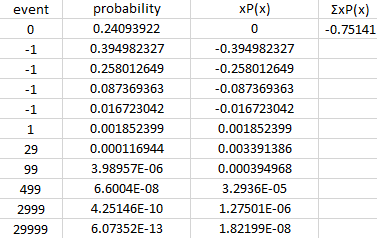
Example of an Excel sheets that I made.
I used a bet of 1 neopoint.
There's my results (the value are rounded to two significant numbers):
2 numbers chosen has an expected profit of -0.71
3 numbers chosen has an expected profit of -0.85
4 numbers chosen has an expected profit of -0.83
5 numbers chosen has an expected profit of -0.86
6 numbers chosen has an expected profit of -0.94
7 numbers chosen has an expected profit of -0.94 (slightly lower than 6 number chosen)
8 numbers chosen has an expected profit of -0.97
9 numbers chosen has an expected profit of -0.71 (very slightly higher than 2 number chosen)
10 numbers chosen has an expected profit of -0.75
What does all that means?
Those number are actually a percentage of the neopoints you will gain (since they are negative, you have a negative gain, so a loss). So, if you choose 10 number, you will lose 75% of the total neopoints you will gamble. You will lose around 71% of the total amount you gamble at Grarrl Keno if you choose nine or two numbers. Nine numbers is slightly better than two, but it is statistically negligible. It's kinda nice to know that if you choose 8 number, you will lose 97% of your total gambled neopoints though. Totally a fair game, am I right?
TL;DR
Grarrl Keno is one of the worst gambling game on Neopets. You have way more chance at Bagatelle, which is inherently rigged. Congratulation TNT for making this huge NP sinks.
Every Excel sheets I made are in the zipped file I uploaded right below. Feel free to point out possible error on my part, I will correct them.
Attached Files
Edited by InsertUsername, 07 February 2018 - 04:51 PM.